一宇宙空间探测器从某一星球的表面垂直升空,假设探测器的质量恒为1 500 kg,发动机的推动力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,下图表示了其速度随时间变化的规律.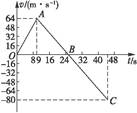
(1)升高后9 s、25 s、45 s,即在图线上A、B、C三点探测器的运动情况如何?
(2)求探测器在该行星表面达到的最大高度.
(3)计算该行星表面的重力加速度及发动机的推动力(假设行星表面没有空气).
相关知识点
一宇宙空间探测器从某一星球的表面垂直升空,假设探测器的质量恒为1 500 kg,发动机的推动力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,下图表示了其速度随时间变化的规律.
(1)升高后9 s、25 s、45 s,即在图线上A、B、C三点探测器的运动情况如何?
(2)求探测器在该行星表面达到的最大高度.
(3)计算该行星表面的重力加速度及发动机的推动力(假设行星表面没有空气).