如图5-15所示,甲、乙两小孩各乘一辆冰车在水平冰面上游戏。甲和他的冰车总质量共为30kg,乙和他的冰车总质量也是30kg。游戏时,甲推着一个质量为15kg的箱子和他一起以2m/s的速度滑行,乙以同样大小的速度迎面滑来。为了避免相撞,甲突然将箱子滑冰面推给乙,箱子滑到乙处,乙迅速抓住。若不计冰面摩擦,求甲至少以多大速度(相对地)将箱子推出,才能避免与乙相撞?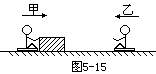
如图5-15所示,甲、乙两小孩各乘一辆冰车在水平冰面上游戏。甲和他的冰车总质量共为30kg,乙和他的冰车总质量也是30kg。游戏时,甲推着一个质量为15kg的箱子和他一起以2m/s的速度滑行,乙以同样大小的速度迎面滑来。为了避免相撞,甲突然将箱子滑冰面推给乙,箱子滑到乙处,乙迅速抓住。若不计冰面摩擦,求甲至少以多大速度(相对地)将箱子推出,才能避免与乙相撞?