如图所示，电源的电动势E＝18V，内阻r=1.0Ω，电阻R2＝5.0Ω，R3＝6.0Ω。平行金属板水平放置，两板间距d＝2cm，当可变电阻R1的滑动头移到R1的中点时，电源的路端电压是16V，一个带电量q=－8.0×10－9C的油滴正好平衡于两板之间。（g＝10m/s2）求：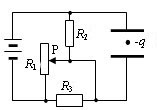
（1）R1的总电阻；
（2）油滴的质量；
（3）移动R1的滑动头P，油滴可获得向下的最大加速度。
如图所示，某货物仓库，需将生产成品用传送带从底端传递到高度为H的高处存放，货物从静止开始轻放到传送带的最下端，已知货物与传送带间的动摩擦因数为μ＝
，传送带始终保持恒定速度运动。若想用最短时间将货物匀加速的运送至顶端，则传送带与水平面夹角θ应设计为多大？最短时间为多少?（传送带长度可随设计需要而变化，g＝10m/s2）
如图所示，坐标系中第一象限有垂直纸面向外的匀强磁场，磁感应强度B=102T，同时有竖直向上与y轴同方向的匀强电场，场强大小E1＝102V/m，第四象限有竖直向上与y轴同方向的匀强电场，场强大小E2＝2E1＝2×102V/m。若有一个带正电的微粒，质量m＝10－12kg，电量q＝10－13C，以水平与x轴同方向的初速度从坐标轴的P1点射入第四象限，OP1＝0.2m，然后从x轴上的P2点穿入第一象限，OP2＝0.4m，接着继续运动。取g＝10m/s2。求：
（1）微粒射入的初速度；
（2）微粒第三次过x轴的位置；
（3）从P1开始到第三次过x轴的总时间。
从某一高处先后落下两个铁球，两球用长35m的细绳相连．第一球降落1s后，第二球开始降落，若不计空气阻力，第二个球下降多长时间细绳刚好被拉直（g取10m/s2）？
一杂技演员，用一只手抛球、接球．他每隔0.40s抛出一球，接到球便立即把球抛出．已知除正在抛、接球的时刻外，空中总有4个球．将球的运动近似看做是竖直方向的运动，球到达的最大高度是（高度从抛球点算起，取
）
如图所示，空间存在垂直纸面向里的两个匀强磁场区域，磁感应强度大小均为B，磁场I宽为L，两磁场间的无场区域为II，宽也为L，磁场III宽度足够大。区域中两条平行光滑金属导轨间距为l，不计导轨电阻，两导体棒ab、cd的质量均为m，电阻均为r。ab棒静止在磁场I中的左边界处，cd棒静止在磁场III中的左边界处，对ab棒施加一个瞬时冲量，ab棒以速度
开始向右运动。
|
（1）求ab棒开始运动时的加速度大小；
（2）若ab棒在区域I运动过程中，cd棒获得的最大速度为
，求ab棒通过区域II的时间；
（3）若ab棒在尚未离开区域II之前，cd棒已停止运动，求ab棒在区域II运动的过程中产生的焦耳热。
粤公网安备 44130202000953号