9月新人教版小升初数学模拟试卷(17)
(1)( +
+ +
+ )÷
)÷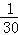 +(
+( +
+ +
+ )÷
)÷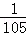 ;
;
(2)2014×(1+0.5)×(1+ )×(1+0.25)×…×(1+
)×(1+0.25)×…×(1+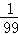 );
);
(3)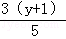 =
=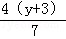 .
.
下列图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为 2cm2,第(2)个图形的面积为 8cm2,第(3)个图形的面积为 18cm2,…,则第(10)个图形的面积为 .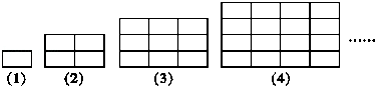
有3个边长为2014的正方形,它们的内部分别镶嵌1个圆、9个等圆和16个等圆.3个正方形内圆面以外的部分的面积从左到右依次是A、B、C,求(A+B)÷C= .
三个容积相同的瓶子里装满了酒精溶液,酒精和水的比分别是1:2、2:3、3:7.当把三瓶酒精溶液混合后,酒精与水的比是 .
规定:如果A大于B,则︳A﹣B︳=A﹣B;如果A等于B,则︳A﹣B︳=0;如果A小于B,则|A﹣B︳=B﹣A.根据上述规律计算:|2013﹣2014︳+︳2014﹣2013︳+︳2014﹣2014︳= .
均匀地向一个瓶子注水,最后把瓶子注满.在注水过程中,水面高度 h 随时间 t 的变化规律如图1,则这个瓶子的形状是如图2中的 .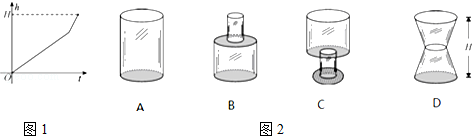
从3、13、17、29、31这五个自然数中,每次取两个数分别作一个分数的分子和分母,一共可组成 个最简分数.
如图有两直线M、N在直线M上有3个点,在直线N上有10个点,把两条真线上所有的点用直线相连,问线M和线N之间最多形成 个交点.
商业街道路两侧有A~F共六家店铺.画阴影的是A店,各店之间的位置关系如图:
(1)A的右边是书店;
(2)书店的前面是花店;
(3)花店的隔壁是面包店;
(4)D店的前面是E店;
(5)E的邻居是酒店;
(6)E跟文具店处在道路的同一侧.
那么,A店是 店.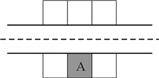
某人沿电车线路行走,每12分钟有一辆电车从后面追上,每4分钟有一辆电车迎面开来.假设两个起点站的发车间隔是相同的,发车间隔是 分.
如图,E、M分别为直角梯形ABCD两边上的点,且DQ、CP、ME彼此平行,若AD=5,CB=7,AE=5,EB=3.阴影部分的面积是 .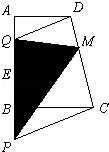
古印度的数学谜题,因诗人郎费罗的介绍而广为流传.下面用现代语言叙述一下:一大群蜜蜂,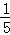 飞向菜花,
飞向菜花,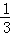 飞往莲花,两小群蜜蜂数量之差的3倍去采蜜,还有10只绕着樱花飞.蜜蜂总数是 只.
飞往莲花,两小群蜜蜂数量之差的3倍去采蜜,还有10只绕着樱花飞.蜜蜂总数是 只.
平平到商场买了甲乙两件商品,甲商品打了四折,乙商品打了六折,正好两件商品所付钱一样多.求平平这次购物打几折.
台球桌上有15个红球,另有六个高分球;黄色球,棕色球,绿色球,蓝色球,粉色球,黑色球,台球比赛规则:
①先打红球,打完所有红球后,再将高分球依次由低分到高分打入袋中,称为打完一局.
②在打进两个红球之间可先后连续打进任意两个高分球,然后再取出这两个高分球放回原处,每打进一个球,选手得到该球的分值.
问:小白兔打完一局最高能得多少分?
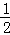 是
是 ; 减少原数的
; 减少原数的 粤公网安备 44130202000953号
粤公网安备 44130202000953号