[河北]2014届河北省沙河市九年级上学期期末联考数学试卷
如图，AB是⊙O的直径，若∠BDC=40°，则∠AOC的度数为（ ）
| A．80° | B．100° | C．140° | D．无法确定 |
过钝角三角形的三个顶点所作圆的圆心在（）
| A．三角形上 | B．三角形外 | C．三角形内 | D．以上皆有可能 |
已知方程（m﹣2）x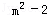
﹣2x+10=0是关于x的一元二次方程，则m的值为（）
| A．2 | B．﹣2 | C．± |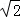
D．±2 |
用配方法解方程2x2﹣8x﹣15=0，配方后的方程是（）
| A．（x﹣2）2="19" | B．（x﹣4）2="31" | C．（x﹣2）2= |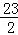
D．（x﹣4）2= |
如图，矩形ABCD∽矩形AFEB，若S矩形ABCD：S矩形AFEB=9：16，AB=6，则S矩形ABCD的值为（）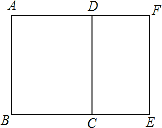
| A．9 | B．16 | C．27 | D．48 |
如图，△ABC的两个顶点BC均在第一象限，以点（0，1）为位似中心，在y轴左方作△ABC的位似图形△AB′C′，△ABC与△A′B′C的位似比为1：2．若设点C的纵坐标是m，则其对应点C′的纵坐标是（）
| A．﹣（2m﹣3） | B．﹣（2m﹣2） | C．﹣（2m﹣1） | D．﹣2m |
已知反比例函数y=﹣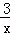
的图象上有两点A（x1，y1），B（x2，y2），若x1＜0＜x2，则下列判断正确的是（）
| A．y1＜y2＜0 | B．0＜y2＜y1 | C．y1＜0＜y2 | D．y2＜0＜y1 |
为了更好保护水资源，造福人类，某工厂计划建一个容积V（m3）一定的污水处理池，池的底面积S（m2）与其深度h（m）满足关系式：V=Sh（V≠0），则S关于h的函数图象大致是（）
A． |
B． |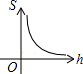
C． |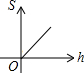
D． |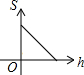
，则sinA的值为（）
用反证法证明命题“在Rt△ABC中，若∠A=90°，则∠B≤45°或∠C≤45°“时，应先假设（）
| A．∠B＞45°，∠C≤45° | B．∠B≤45°，∠C＞45° | C．∠B＞45°，∠C＞45° | D．∠B≤45°，∠C≤45° |
如图，一个圆形转盘被等分成八个扇形区域，上面分别标上1，3，4，5，6，7，8，9，转盘可以自由转动，转动转盘一次，指针指向的数字为偶数所在区域的概率是（）
A． |
B． |
C． |
D． |
如图是二次函数y=ax2+bx+c（a≠0）的图象，则下列说法中正确的是（）
| A．A＞0 | B．4a+b＞0 | C．c="0" | D．A+b+c＞0 |
下列说法中不正确的是（）
| A．若点A在半径为r的⊙O外，则OA＜r |
| B．相切两圆的切点在两圆的连心线上 |
| C．三角形只有一个内切圆 |
| D．相交两圆的连心线垂直平分其公共弦 |
为了解2013年河北中考数学试卷学生得分情况，某小组从中随机抽查了1000份进行分析，下列说法中不正确的是（）
| A．以上调查方式属于抽样调查 | B．总体是所有考生的数学试卷 |
| C．个体指每个考生的数学试卷 | D．样本容量指所有抽取的1000份试卷 |
如图，放映幻灯时，通过光源，把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20cm，到屏幕的距离为60cm，且幻灯片中的图形的高度为6cm，则屏幕上图形的高度为_________cm．
在一个不透明的布袋中装有除颜色外其余都相同的红、黄、蓝球共200个，墨墨通过多次摸球试验后发现，其中摸到红色球和蓝色球的频率稳定在25%和55%，则口袋中可能有黄球_________个．
如图，二次函数y=ax2+bx+c（a≠0）的图象过原点O，且该图象的对称轴是直线x=
，若函数值y＞0．则x取值范围是_________．
如图为一个表面分别标有：“A”、“B”、“C”、“D”、“E”、“F”六个字母的正方体的平面展开图如图，则与字母“B”所在的面字相对的面上标有字母“_________”．
按要求完成下列各小题
（1）解方程；4x2﹣3
x+3=0；
（2）计算：（sin45°）2+2cos60°﹣tan45°．
如图，反比例函数y=
（k≠0）的图象过等边三角形AOB的顶点A，已知点B（﹣2，0）
（1）求反比例函数的表达式；
（2）若要使点B在上述反比例函数的图象上，需将△ABC向上平移多少个单位长度？
现有九张背面一模一样的扑克牌，正面分别为：红桃A、红桃2、红桃3、红桃4、黑桃A、黑桃2、黑桃3、黑桃4、黑桃5．
（1）现将这九张扑克牌混合均匀后背面朝上放置，若从中摸出一张，求正面写有数字3的概率是多少？
（2）现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置，并将红桃正面数字记作m，黑桃正面数字记作n，若从黑桃和红桃中各任意摸一张，求关于x的方程mx2+3x+
=0有实根的概率．（用列表法或画树形图法解，A代表数字1）
如图，AB是⊙O的直径，C是⊙O上的一点，DA与⊙O相切于点A，DA=DC=
．
（1）求证：DC是⊙O的切线；
（2）若∠CAB=30°，求阴影部分的面积．
如图，在直角梯形ABCD中，AD∥BC，∠A=90°，BD⊥CD，垂足为D．
（1）若AD=9，BC=16，求BD的长；
（2）求证：AB2•BC=CD2•AD．
某相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品，根据市场调研，发现如下两种信息：
信息一：销售甲款护肤品所获利润y（元）与销售量x（件）之间存在二次函数关系y=ax2+bx．在x=10时，y=140；当x=30时，y=360．
信息二：销售乙款护肤品所获利润y（元）与销售量x（件）之间存在正比例函数关系y=3x．请根据以上信息，解答下列问题；
（1）求信息一中二次函数的表达式；
（2）该相宜本草护肤品专柜计划在春节前夕促销甲、乙两款护肤品共100件，请设计一个营销方案，使销售甲、乙两款护肤品获得的利润之和最大，并求出最大利润．
粤公网安备 44130202000953号