[山东]2013年初中毕业升学考试(山东青岛卷)数学
“十二五”以来,我国积极推进国家创新体系建设,国家统计局《2012年国民经济和社会发展统计公报》指出,截止2012年底,国内有效专利达8750000件,将8750000件用科学计数法表示为件
A.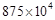 |
B.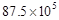 |
C.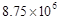 |
D.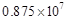 |
一个不透明的口袋里装有除颜色都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法,先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球,因此小亮估计口袋中的红球大约有个
| A.45 | B.48 | C.50 | D.55 |
已知矩形的面积为36cm2,相邻的两条边长为xcm和ycm,则y与x之间的函数图像大致是
A. |
B.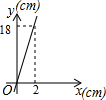 |
C. |
D.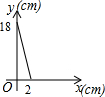 |
如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为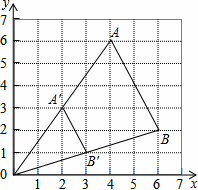
A、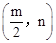 B、(m,n) C、
B、(m,n) C、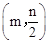 D、
D、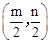
某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下: ,
, ,
, ,
, ,则这两名运动员中的 的成绩更稳定。
,则这两名运动员中的 的成绩更稳定。
某企业2010年底缴税40万元,2012年底缴税48.4万元,设这两年该企业缴税的年平均增长率为x,根据题意,可得方程 .
要把一个正方体分割成8个小正方体,至少需要切3刀,因为这8个小正方体都只有三个面现成的,其它三个面必须用刀切3次才能切出来,那么,要把一个正方体分割成27个小正方体,至少需要要刀切 次,分割成64个小正方体,至少需要用刀切 次。
已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点
求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等(在题目的原图中完成作图)
结论:
请根据所给信息,帮助小颖同学完成她的调查报告
2013年4月光明中学八年级学生每天干家务活平均时间的调查报告
| 调查目的 |
了解八年级学生每天干家务活的平均时间 |
||||||||||||||||||||||||||||||
| 调查内容 |
光明中学八年级学生每天干家务活的平均时间 |
||||||||||||||||||||||||||||||
| 调查方式 |
抽样调查 |
||||||||||||||||||||||||||||||
| 调查步骤 |
1、数据的收集: (1)在光明中学八年级每班随机调查5名学生; (2)统计这些学生2013年4月每天干家务活的平均时间(单位:min),结果如下(其中A表示10min;B表示20min;C表示30min);
2、数据的处理: |
||||||||||||||||||||||||||||||
| 调查结论 |
光明中学八年级共有240名学生,其中大约有 名学生每天干家务活的平均时间是20min …… |
小明和小刚做纸牌游戏,如图,两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各抽取一张,称为一次游戏。当两张牌的牌面数字之和为奇数,小明得2分,否则小刚得1分,这个游戏对双方公平吗?请说明理由
某校学生捐款支援地震灾区,第一次捐款总额为6600元,第二次捐款总额为7260元,第二次捐款人数比第一次多30人,而且两次人均捐款额恰好相等,求第一次的捐款人数
如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市。CD与AB所在直线互相平行,且都与马路两边垂直,马路宽20米,A,B相距62米,
∠A=67°,∠B=37°
(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米
(参考数据: )
)
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
在前面的学习中,我们通过对同一面积的不同表达和比较,根据图①和图②发现并验证了平方差公式和完全平方公式
这种利用面积关系解决问题的方法,使抽象的数量关系因集合直观而形象化。
【研究速算】
提出问题:47×43,56×54,79×71,……是一些十位数字相同,且个位数字之和是10的两个两位数相乘的算式,是否可以找到一种速算方法?
几何建模:
用矩形的面积表示两个正数的乘积,以47×43为例:
(1)画长为47,宽为43的矩形,如图③,将这个47×43的矩形从右边切下长40,宽3的一条,拼接到原矩形的上面。
(2)分析:原矩形面积可以有两种不同的表达方式,47×43的矩形面积或(40+7+3)×40的矩形与右上角3×7的矩形面积之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021,用文字表述47×43的速算方法是:十位数字4加1的和与4相乘,再乘以100,加上个位数字3与7的积,构成运算结果。
归纳提炼:
两个十位数字相同,并且个位数字之和是10的两位数相乘的速算方法是(用文字表述) .
【研究方程】
提出问题:怎么图解一元二次方程
几何建模:
(1)变形:
(2)画四个长为 ,宽为
,宽为 的矩形,构造图④
的矩形,构造图④
(3)分析:图中的大正方形面积可以有两种不同的表达方式, 或四个长
或四个长 ,宽
,宽 的矩形之和,加上中间边长为2的小正方形面积
的矩形之和,加上中间边长为2的小正方形面积
即: 
∵
∴
∴
∵
∴
归纳提炼:求关于 的一元二次方程
的一元二次方程 的解
的解
要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
【研究不等关系】
提出问题:怎么运用矩形面积表示 与
与 的大小关系(其中
的大小关系(其中 )?
)?
几何建模:
(1)画长 ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割
(2)变形:
(3)分析:图⑤中大矩形的面积可以表示为 ;阴影部分面积可以表示为
;阴影部分面积可以表示为 ,
,
画点部分的面积可表示为 ,由图形的部分与整体的关系可知:
,由图形的部分与整体的关系可知: >
> ,即
,即 >
>
归纳提炼:
当 ,
, 时,表示
时,表示 与
与 的大小关系
的大小关系
根据题意,设 ,
, ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
已知,如图, ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)当t为何值时,四边形AQDM是平行四边形?
(2)设四边形ANPM的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM的面积是 ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
ABCD面积的一半,若存在,求出相应的t值,若不存在,说明理由
(4)连接AC,是否存在某一时刻t,使NP与AC的交点把线段AC分成 的两部分?若存在,求出相应的t值,若不存在,说明理由
的两部分?若存在,求出相应的t值,若不存在,说明理由
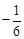
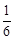



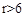
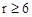
 .
. 的图像相交于点P,则这个正比例函数的表达式是 .
的图像相交于点P,则这个正比例函数的表达式是 .




 粤公网安备 44130202000953号
粤公网安备 44130202000953号