[辽宁]2012年初中毕业升学考试(辽宁沈阳卷)数学
沈阳地铁2号线的开通,方便了市民的出行.从2012年1月9日到2月7日的30天里,累计客运量约达3040000人次,将3040000用科学记数法表示为【 】
| A.3.04×105 | B.3.04×106 | C.30.4×105 | D.0.304×10721 |
在平面直角坐标系中,点P (-1,2 ) 关于x轴的对称点的坐标为【 】
| A.(-1,-2 ) | B.(1,-2 ) | C.(2,-1 ) | D.(-2,1 ) |
气象台预报“本市明天降水概率是30%” ,对此消息下列说法正确的是【 】
| A.本市明天将有30%的地区降水 |
| B.本市明天将有30%的时间降水 |
| C.本市明天有可能降水 |
| D.本市明天肯定不降水 |
一次函数y=-x+2的图象经过【 】
| A.一、二、三象限 | B.一、二、四象限 | C.一、三、四象限 | D.二、三、四象限 |
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有【 】
| A.4个 | B.6个 | C.8个 | D.10个 |
已知点A为双曲线y= 图象上的点,点O为坐标原点过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为 .
图象上的点,点O为坐标原点过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为 .
.有一组多项式:a+b2,a2-b4,a3+b6,a4-b8,…,请观察它们的构成规律,用你发现的规律写出第10个多项式为 .
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为 _cm2.
小丁将中国的清华大学、北京大学及英国的剑桥大学的图片分别贴在3张完全相同的不透明的硬纸板上,制成名校卡片,如图.小丁将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,放回后洗匀,再随机抽取一张卡片.
(1) 小丁第一次抽取的卡片上的图片是剑桥大学的概率是多少?(请直接写出结果)
(2) 请你用列表法或画树状图(树形图) 法,帮助小丁求出两次抽取的卡片上的图片一个是国内大学、一个是国外大学的概率.(卡片名称可用字母表示)
已知,如图,在荀ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
为了提高沈城市民的节水意识,有关部门就“你认为最有效的节水措施”随机对部分市民进行了问卷调查.其中调查问卷设置以下选项(被调查者只能选择其中的一项 ):
| A.出台相关法律法规; |
| B.控制用水大户数量; |
| C.推广节水技改和节水器具; |
| D.用水量越多,水价越高; |
E.其他.根据调查结果制作了统计图表的一部分如下:
(1)此次抽样调查的人数为①人;
(2)结合上述统计图表可得m=②,n=③;
(3)请根据以上信息直接在答题卡中补全条形统计图.
甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD. 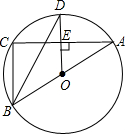
(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
已知,如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式;
(2)点C为线段OB上一动点 (点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示);
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.
已知,如图①,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),且AB= ,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.
,在∠MON的内部、△AOB的外部有一点P,且AP=BP,∠APB=120°.
(1)求AP的长;
(2)求证:点P在∠MON的平分线上;
(3) 如图②,点C,D,E,F分别是四边形AOBP的边AO,OB,BP,PA的中点,连接CD,DE,EF,FC,OP.①当AB⊥OP时,请直接写出四边形CDEF的周长的值;②若四边形CDEF的周长用t表示,请直接写出t的取值范围.
已知,如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为 (0,2 ),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C为y轴正半轴上一点,且OC=AB,抛物线y= x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.
(1) 求此抛物线的函数表达式;
(2) 求证:∠BEF=∠AOE;
(3) 当△EOF为等腰三角形时,求此时点E的坐标;
(4) 在(3)的条件下,当直线EF交x轴于点D,P为(1) 中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的( ) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
) 倍.若存在,请直接写出点P的坐标;若不存在,请说明理由.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.



 的解集是 .
的解集是 . +2sin45°
+2sin45° 粤公网安备 44130202000953号
粤公网安备 44130202000953号