[浙江]2011-2012学年度浙江省桐乡市高三下学期二月模拟物理卷
为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示。当此车加速上坡时,乘客 
| A.处于失重状态 |
| B.不受摩擦力的作用 |
| C.受到向前(水平向右)的摩擦力作用 |
| D.所受力的合力竖直向上 |
如图为通过理想变压器将高压电降压后供居民使用示意图,其中R0 表示导线总电阻,如果用户数增加,下列说法正确的是
| A.电压表V1示数增大 |
| B.电压表V2示数不变 |
| C.电阻R0损耗功率增大 |
| D.变压器输入功率不变 |
如图所示,一横截面为直角三角形的三棱镜,∠B=900,∠C=300。一束与AB面成θ=300角的光线射向AB面,经过BC边一次反射,再从AC边射出,且出射光线的折射角为600。则这种材料的折射率为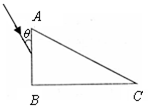
A. |
B. |
C.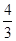 |
D.2 |
如图所示,a、b是一个点电荷形成的电场中同一等势面上的两 点,c、d是另一等势面上的两点。实线acb和adb分别是甲、乙 两带电粒子的运动轨迹。已知两粒子在a点时具有相同的动能,下列判断正 确的是
| A.甲、乙两粒子可能带同种电荷 |
| B.两粒子经过b点时具有相同的电势能 |
| C.甲粒子经过c点时与乙粒子经过d点时具有相同的动能 |
| D.若取无穷远处为零电势,则甲粒子经过c点时电势能小于乙粒子经过d点 |
时的电势能
2011年11月初,我国“神州八号”飞船成功发射并与“天宫一号”目标飞行器顺利对接。若“神州八号”变轨前后均可看做匀速圆周运动,则“神州八号”从低轨道变轨到高轨道与“天宫一号”对接前后,下列说法正确的是
| A.“神州八号”应向前喷气 |
| B.“神州八号”应向后喷气 |
| C.变轨后“神州八号”运行速度增大 |
| D.变轨后“神州八号”运行周期增大 |
一列简谐横波沿x轴的正方向传播,已知t=0时刻,此波刚好传播到x=5米处,如图所示,质点P位于x=1米处,P点至少再经过0.3s才能到达波峰处,Q点为x=9米处,则以下说法正确的是
| A.这列波的波长是5m |
| B.这列波的波速是10m/s |
| C.质点Q要经过0.7s才能第一次到达波峰处 |
| D.质点Q到达波峰处时质点P也恰好到达波峰处 |
如图所示,ACD、EFG为两根相距L的足够长的金属直角导轨,它们被竖直固定在绝缘水平面上,CDGF面与水平面成θ角。两导轨所在空间存在垂直于CDGF平面向上的匀强磁场,磁感应强度大小为B。两根质量均为m、长度均为L的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为μ,两金属细杆的电阻均为R,导轨电阻不计。当ab以速度v1沿导轨向下匀速运动时,cd杆也正好以速度v2向下匀速运动。重力加速度为g。以下说法正确的是 
A.回路中的电流强度为
B.ab杆所受摩擦力为mgsinθ
C.cd杆所受摩擦力为
D.μ与v1大小的关系为
某研究性学习小组用如图(a)所示装置验证机械能守恒定律。让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即 ,但直接测量摆球到达B点的速度v比较困难,现利用平抛的特性来间接地测出v。
,但直接测量摆球到达B点的速度v比较困难,现利用平抛的特性来间接地测出v。
如图(a)中,悬点正下方一竖直立柱上 放置一个与摆球完全相同的小球(OB等于摆线长),当悬线摆至B处,摆球与小球发生完全弹性碰撞(速度互换),被碰小球由于惯性向前飞出作平抛运动。在地面上放上白纸,上面覆盖着复写纸,当小球落在复写纸上时,会在下面白纸上留下痕迹。用重锤线确定出A、B点的投影点N、M。重复实验10次(小球每一次都从同一点由静止释放),球的落点痕迹如图(b)所示,图中米尺水平放置,零刻度线与M点对齐。用米尺量出AN的高度h1、BM的高度h2,算出A、B两点的竖直距离,再量出M、C之间的距离x,即可验证机械能守恒定律。(已知重力加速度为g,两球的质量均为m。)
(1)根据图(b)可以确定小球平抛时的水平射程为 m。
(2)用题中所给字母表示出小球平抛时的初速度v0 = 。
(3)此实验中,小球从A到B过程重力势能的减少量ΔEP = ,动能的增加量EK=
若要验证此过程中摆球的机械能守恒,实验数据应满足一个怎样的关系 。(用题中的符号表示)
在做“测定电池的电动势和内阻”的实验中,一学生按图电路进行连接(如图甲所示),共用6根导线,即aa'、bb'、cc'、dd'、eb'、df。由于混进一根内部断开的导线,所以合上开关后,发现两个电表的指针都不偏转。他用万用表电压档测量ab'间电压时,读数约为3.0V(已知电池的电动势约为3.0V)。
在进行该实验的过程中,该同学已经根据原理图完成部分导线的连接(如图乙所示),请在实物接线图中完成余下的导线连接;
为了进一步判定哪一条导线断路,你认为还必须再测哪两点间的电压,并简要说明理由?
该学生将断的导线换掉后,测出了如下表中的5组U、I值,请你在图示的坐标纸上画出U-I图线,并根据图线求得该电池的电源电动势E= V,内阻r= Ω。



某研究性学习小组为了测量木头与铁板间动摩擦因数,利用如图所示的装置将一铁板静置于水平地面上,其中水平段AB长L1=1.0m,倾斜段CD长L2=0.5m,与水平面夹角θ=530, BC是一小段圆弧,物体经过BC段速度大小不变。现将一小木块(可视为质点)从斜面上的P点由静止开始释放,木块滑到水平面上Q点处停止运动。已知P点距水平面高h=0.2m,B、Q间距x=0.85m,(取重力加速度g=10m/s2,sin530="0.8) " 求:
动摩擦因数μ;
若某同学在A点以v0=2.5m/s的初速度将木块推出,试通过计算说明木块能否经过P点?若不能,则请求出木块从A点出发运动到最高点所需时间t。
如图所示,在xoy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与负x轴成45°角。在x<0且OM的左侧空间存在着负x方向的匀强电场,场强E大小为32N/C;在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场,磁感应强度B大小为0.1T。一不计重力的带负电的微粒,从坐标原点O沿y轴负方向以v0=2×103m/s的初速度进入磁场,最终离开电、磁场区域。已知微粒的电荷量q=5×10-18C,质量m=1×10-24kg,求: 
带电微粒第一次经过电、磁场边界OM的坐标;
带电微粒在磁场区域运动的总时间;
带电微粒最终离开电、磁场区域的位置坐标。
荡秋千是一项古老的运动,秋千是一块板用两根绳系在两个固定的悬点组成,设某人的质量为m,身高为H,站立时重心离脚底H/2,蹲下时重心离脚底H/4,绳子悬挂点到踏板的绳长为6H,绳子足够柔软且不可伸长,绳子和踏板的质量不计,人身体始终与绳子保持平行,重力加速度为g。若该人在踏板上保持站式,由伙伴将其推至摆角θ0(单位:rad),由静止释放,忽略空气阻力,求摆至最低点时每根绳的拉力大小;
若该人在踏板上保持站式,由伙伴将其推至摆角θ1(单位:rad),由静止释放,摆至另一侧最大摆角为θ2(单位:rad),设空气阻力大小恒定,作用点距离脚底为H/3,求空气阻力的大小。
若该人在踏板上采取如下步骤:当荡至最高处时,突然由蹲式迅速站起,而后缓缓蹲下,摆至另一侧最高处时已是蹲式,在该处又迅速站起,之后不断往复,可以荡起很高。用此法可以荡起的最大摆角为θm 弧度,假设人的“缓缓蹲下”这个动作不会导致系统机械能的损耗,而且空气阻力大小和作用点与第(2)问相同,试证明:
 。
。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号