[广东]2011年广东省揭阳立才中考模拟数学卷
一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是
如图,已知抛物线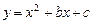 的对称轴为
的对称轴为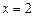 ,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为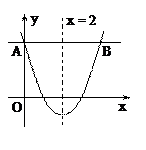
| A.(2,3) | B.(3,2) |
| C.(3,3) | D.(4,3) |
|
甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
| 分数 |
7 分 |
8 分 |
9 分 |
10 分 |
| 人数 |
11 |
0 |
|
8 |

在图1中,“7分”所在扇形的圆心角
等于 °.
请你将图2的统计图补充完整.
经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?

如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.求直线DE的解析式和点M的坐标;
若反比例函数
 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;若反比例函数
 (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
在图1至图3中,直线MN与线段AB相交于点O,∠1 = ∠2 = 45°.
如图15-1,若AO = OB,请写出AO与BD 的数量关系和位置关系;
将图15-1中的MN绕点O顺时针旋转得到图15-2,其中AO = OB.
求证:AC = BD,AC ⊥ BD;将图15-2中的OB拉长为AO的k倍得到图15-3,求
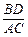 的值.
的值.
如图,在直角梯形ABCD中,AD∥BC,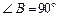 ,AD = 6,BC = 8,
,AD = 6,BC = 8,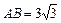 ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
设点P,Q运动的时间是t秒(t>0).设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
当BP = 1时,求△EPQ与梯形ABCD重叠部分的面积.
随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.

某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.
若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y = x+150,
x+150,
成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元)(利润 = 销售额-成本-广告费).
若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为
常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费).
x2 元的附加费,设月利润为w外(元)(利润 = 销售额-成本-附加费).当x = 1000时,y =" " 元/件,w内 =" " 元;
分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
 2) 的结果是
2) 的结果是





 < 4的解集表示在数轴上,正确的是
< 4的解集表示在数轴上,正确的是

 的结果是
的结果是







 的相反数是 .
的相反数是 . ,则点B所对应的数为 .
,则点B所对应的数为 . 的一个根,则
的一个根,则  的值为 .
的值为 . ,
, ,则圆锥的底面积是 平方米(结果保留π).
,则圆锥的底面积是 平方米(结果保留π).
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号