小升初数学攻克难点真题-探索规律
六(2)班的同学在布置“六•一”节联欢会场时,将180只彩色灯泡按5个红色,4个黄色,3个蓝色的顺序连成一排,那么这排彩色灯泡中:
(1)黄色灯泡有 个.
(2) 灯泡的个数最少.
(3)蓝色灯泡的个数是红色灯泡个数的 .
.
儿童节用小灯泡布置教室,按“三红、二黄、二绿”规律连接起来,第2010个小灯泡是( )色.
A. 红 B. 绿 C. 黄
有一根1米长的木条,第一次据掉它的 ,第二次据掉余下的
,第二次据掉余下的 ,第三次据掉余下的
,第三次据掉余下的 ,…,这样下去,最后一次据掉余下的
,…,这样下去,最后一次据掉余下的 ,这根木条最后剩( )
,这根木条最后剩( )
A. 米 米 |
B. 米 米 |
C. 米 米 |
D. 米 米 |
已知0.123456789101112131415…是一个有规律的小数.
(1)小数点后第100位上的数字是 数.(填奇或偶)
(2)小数点后第100位上的数字大小是 .
(3)探究并填空:小数点后第100位前(包括第100位)的数字之和是 .
编号为1至10的十个果盘中,每盘都盛有水果,共盛放100个.其中第一盘里有16个,并且编号相邻的三个果盘中水果数的和都相等,求第8盘中水果最多可能有几个.
用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼( )个正方形.
| A.6 | B.7 | C.8 | D.9 |
如果按照下面的画法,画到第10个正方形时,图中共有( )个直角三角形.
| A.28 | B.32 | C.36 | D.40 |
把边长为1厘米的正方形纸片,按如图的规律拼成长方形;

(1)用6个正方形拼成的长方形周长是 厘米;
(2)用n个正方形拼成的长方形周长是 厘米.
认真观察多边形的“边”与“角”的关系,回答下列问题:
| 多边形 |
 |
 |
 |
 |
… |
| 边数 |
3 |
4 |
5 |
6 |
… |
| 内角和 |
180° |
360° |
|
|
… |
(1)多边形的内角和与它的边数的关系是 ;
(2)一个8边形的内角和是 度,一个n边形的内角和是 度.
如图是用棋子摆成的“上”字:第一个“上”字,第二个“上”字,第三个“上”字,如果按照以上规律继续摆下去,那么通过观察,可以发现:第90个“上”字分别需要 枚棋子.
分析推理找规律
点数



增加条数 ﹣﹣ 2 3 4
总条数 1 3 6 10
根据上表的规律,20个点能连成 条线段,n个点能连成 条线段.
准备(1)每个  都是棱长为1厘米的正方体.
都是棱长为1厘米的正方体.
(2)一个挨着一个排成一排
你要研究的问题是:正方体个数与拼成的长方体表面积之间的关系.
探索过程:个数 图形 表面积(平方厘米)

根据你的发现填空.
当正方体个数为10时,所拼成的长方体表面积是 平方厘米.
当正方体个数为a时,所拼成的长方体表面积是 平方厘米.
当拼成的长方体表面积是202平方厘米时,正方体个数是 .
探寻规律.

如图是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个2×2的正方形图案(如图‚),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图ƒ),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个10×10的正方形图案,则其中完整的圆共有 个.
一列数1,2,2,3,3,3,4,4,4,4,….中的第35个数为( )
| A.6 | B.7 | C.8 | D.无答案 |
填在下面各正方形中的四个数之间都有相同的规律,根据规律,m的值是( )
| A.86 | B.52 | C.38 | D.74 |
在1、3、7、15、31、( )、127…这一串数中,括号中的数应该是( )
A. 46 B. 60 C. 63
找规律:2,3,4,6,6,9,8,12,10,15,( )正确选项是( )
| A.10,12 | B.10,18 | C.12,15 | D.12,18 |
观察表一,寻找规律.表二是从表一剪下的一部分,则a=( )
| |
0 |
1 |
2 |
3 |
… |
| |
1 |
3 |
5 |
7 |
… |
| |
2 |
5 |
8 |
11 |
… |
| |
3 |
7 |
11 |
15 |
… |
| … |
… |
… |
… |
… |
|
表一
| 17 |
20 |
| 23 |
a |
表二.
A. 24 B. 25 C. 26 D. 27
在下面的数表中,每隔两个数后的第三个数就会被圈起来.如果按照相同的方式继续圈下去,下列( )应该被圈起来.
| A.100 | B.101 | C.102 | D.103 |
一个自然数表如下(零除外,表中下一行数的个数是上一行的2倍),第六行最后一个数是( )
第一行 1
第二行 2 3
第三行 4 5 6 7
… …
| A.31 | B.63 | C.64 | D.127 |
如图,不同的图形代表不同的数,方格外的数分别表示所在的这一行或这一列中全体图形所代表的数之和,比如第二行中“7=○+◇”,根据图示所表示的关系,可以推算出?= .

为了学生的身体健康,学校课桌、凳子的高度都是按照一定的关系科学设计.小明对学校所添置的一批课桌、凳子进行观察研究,发现他们可以根据人的身长调节高度,于是他测量了一套课桌、凳子上的对应的其中四档的高度,得到数据如下表:
档次
高度 第一档 第二档 第三档 第四档
凳子高x(厘米) 37.0 40.0 42.0 45.0
课桌高y(厘米) 70.0 74.8 78.0 82.8
(1)小明经过对数据探究,发现课桌高y与凳子高x之间存在某种变化规律,请你通过探究找出一个式子来表示它们之间的变化规律.
(2)小明回家后测量了家里的写字台和凳子,写字台的高度为77厘米,凳子的高度为43.5厘米,请你判断它们是否配套,并说明理由.
如图,○、△、□各表示一个两位数中的其中一个数字,观察下面图与数的关系,第4图形表示的两位数是( )

A. 54 B. 43 C. 34
小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由( )个小正方体拼成.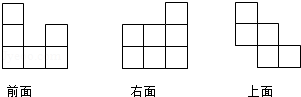
| A.8 | B.9 | C.10 | D.11 |
把1﹣40各数按如图所示的方法排列起来,用一个长方形框出其中的6个数,这6个数的和可以是90或87.那么在此图中,像这样共可以框出 个不同的和.

观察下列各算是:1+3=4=2的平方,1+3+5=9=3的平方,1+3+5+7=16=4的平方…按此规律:
(1)试猜想:1+3+5+7+…+2005+2007= ;
(2)推广:1+3+5+7+9+…+(2n﹣1)+(2n+1)= .
我们一起来计算:
1+3= = 2;
1+3+5= = 2;
1+3+5+7= = 2;
1+3+5+7+9= = 2;
根据以上规律填空:1+3+5+…+19= ;
如果1+3+5+…+(2n﹣1)=225(n是一个整数),那么n的值等于多少?
先找出规律,再把下面的算式填写完整.计算下面三组算式,在横线里填上“>”、“<’’或“=”.
(1)

(2)

(3) ﹣
﹣
 ×
×
根据找到的规律,把下面的算式填完整.
(3) ﹣
﹣ =
= ×
×
(4) ﹣
﹣ =
= ×
× .
.
找规律,填一填.
22﹣12=3 32﹣22=5 72﹣62=13 992﹣982=
你也举一个这样的例子吧. ﹣ = .
一次大型运动会上,工作人员按照3个红气球,2个黄气球,1个绿气球的顺序把气球穿起来装饰运动场,那么第2013个气球是 颜色的(填“红”、“黄”或“绿”)
小朋友们用小木棒摆图形,如图:

摆1个用6根,摆2个用11根,摆3个用16根…摆10个用 根,摆 个用小棒101根.
有一根弯曲的铁丝如下图1.按下面的虚线剪切,把铁丝分成几段.
(1)在括号里填写适当的数.

图1 (4)段 段 段
(2)剪切5次,把铁丝分成几段?剪切10次呢?
(3)猜想:按照上面的方法剪切多少次时,铁丝分成70段?






 化成小数后,小数点后第1980位上的数字是 .
化成小数后,小数点后第1980位上的数字是 .

 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 …
… 开始,前407个分数的和是多少?
开始,前407个分数的和是多少?



 .
. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, …
… 是此串分数中的第多少个分数?
是此串分数中的第多少个分数?






 ,所以
,所以 .
.
 ,所以
,所以 =
= .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号