高三物理第八套
一质量为m的物块恰好静止在倾角为 的斜面上。现对物块施加一个竖直向下的恒力F,如图所示。则物块
的斜面上。现对物块施加一个竖直向下的恒力F,如图所示。则物块
| A.仍处于静止状态 |
| B.沿斜面加速下滑 |
| C.受到的摩擦力不便 |
| D.受到的合外力增大 |
质点做直线运动的位移x与时间t的关系为x =" 5t" + t2(各物理量均采用国际单位制单位),则该质点
| A.第1s内的位移是5m |
| B.前2s内的平均速度是6m/s |
| C.任意相邻1s内的位移差都是1m |
| D.任意1s内的速度增量都是2m/s |
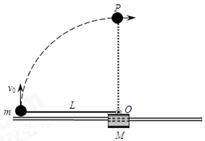
一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径。现将一物体沿与水平面成α角的方向已速度υ0抛出,如图(b)所示。则在其轨迹最高点P处的曲率半径是
A. |
B. |
C. |
D. |
图(a)为示管的原理图。如果在电极YY’之间所加的电压图按图(b)所示的规律变化,在电极XX’之间所加的电压按图(c)所示的规律变化,则在荧光屏上会看到的图形是

如图所示的区域内有垂直于纸面的匀强磁场,磁感应强度为B。电阻为R、半径为L、圆心角为45°的扇形闭合导线框绕垂直于纸面的O轴以角速度ω匀速转动(O轴位于磁场边界)。则线框内产生的感应电流的有效值为

A. B.
B. C.
C. D.
D.
如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处。若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上。则t0可能属于的时间段是

A. B.
B. C.
C. D.
D.
为了测量某一弹簧的劲度系数,降该弹簧竖直悬挂起来,在自由端挂上不同质量的砝码。实验册除了砝码的质量m与弹簧长度l的相应数据,七对应点已在图上标出。(g=9.8m/s2)
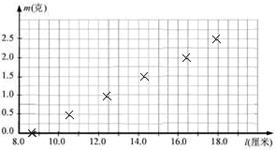
(1)作出m-l的关系图线;
(2)弹簧的劲度系数为 N/m.
某同学实用多用电表粗略测量一定值电阻的阻值,先把选择开关旋到“×1k”挡位,测量时针偏转如图(a)所示。请你简述接下来的测量过程:
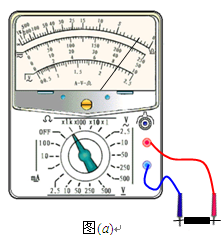
① ;
② ;
③ ;
④测量结束后,将选择开关旋到“OFF”挡。
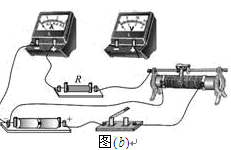
(2)接下来采用“伏安法”较准确地测量该电阻的阻值,所用实验器材如图(b)所示。
其中电压表内阻约为5k ,电流表内阻约为5 。图中部分电路已经连接好,请完成实验电路的连接。
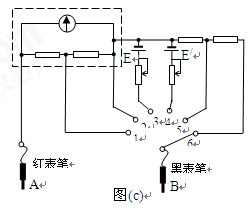
(3)图(c)是一个多量程多用电表的简化电路图,测量电流、电压和电阻各有两个量程。当转换开关S旋到位置3时,可用来测量 ;当S旋到位置 时,可用来测量电流,其中S旋到位置 时量程较大。
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即 ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
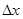 所用的时间为
所用的时间为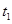 ,紧接着通过下一段位移
,紧接着通过下一段位移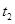 .则物体运动的加速度为
.则物体运动的加速度为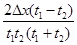
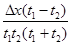
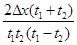
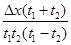
 粤公网安备 44130202000953号
粤公网安备 44130202000953号