专题52 数字变化类规律性问题(预测题)
把所有正偶数从小到大排列,并按如下规律分组:(2,4),(6,8,10,12),(14,16,18,20,22,24),…,现用等式AM=(i,j)表示正偶数M是第i组第j个数(从左往右数),如A10=(2,3),则A2014=( )
| A.(31,15) | B.(31,16) | C.(32,15) | D.(32,16) |
来源:专题52 数字变化类规律性问题(预测题)
观察规律:1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,则2+6+10+14+…+2014的值是 。
来源:专题52 数字变化类规律性问题(预测题)
观察下列各数的个位数字的变化规律:21=2,22=4,23=8,24=16,25=32,26=64……通过观察,你认为22011的个位数字应该是
来源:专题52 数字变化类规律性问题(预测题)
让我们轻松一下,做一个数字游戏:
第一步:取一个自然数n1=5,计算n12+1得a1;
第二步:算出a1的各位数字之和得n2,计算n22+1得a2;
第三步:算出a2的各位数字之和得n3,计算n32+1得a3;
…………
依此类推,则a2008=___ __.
来源:专题52 数字变化类规律性问题(预测题)
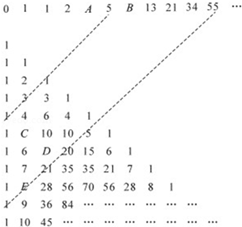
 ,
, ,
, ,…
,… 的结果为 (写成一个分数的形式)
的结果为 (写成一个分数的形式) 粤公网安备 44130202000953号
粤公网安备 44130202000953号