小学奥数几何专题——圆与扇形
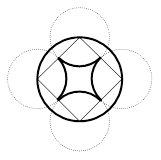
图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?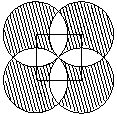
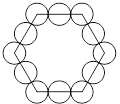
如右图,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.则花瓣图形的面积是多少平方厘米?( 取3)
取3)
如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧.求阴影部分面积.(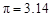 )
)
如图,大小两圆的相交部分(即阴影区域)的面积是大圆面积的 ,是小圆面积的
,是小圆面积的 .如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?
.如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?
如图,边长为12厘米的正五边形,分别以正五边形的5个顶点为圆心,12厘米为半径作圆弧,请问:中间阴影部分的周长是多少?( )
)
如图,大圆半径为小圆的直径,已知图中阴影部分面积为 ,空白部分面积为
,空白部分面积为 ,那么这两个部分的面积之比是多少?(圆周率取
,那么这两个部分的面积之比是多少?(圆周率取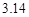 )
)
用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?
如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.(圆周率取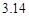 )
)
如下图所示, 是半圆的直径,
是半圆的直径, 是圆心,
是圆心, ,
, 是
是 的中点,
的中点, 是弦
是弦 的中点.若
的中点.若 是
是 上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是多少平方厘米.
上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是多少平方厘米.
图中给出了两个对齐摆放的正方形,并以小正方形中右上顶点为圆心,边长为半径作一个扇形,按图中所给长度阴影部分面积为多少?( )
)
如图,图形中的曲线是用半径长度的比为 的6条半圆曲线连成的.问:涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少?
的6条半圆曲线连成的.问:涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少?
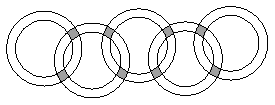
奥运会的会徽是五环图,一个五环图是由内圆直径为6厘米,外圆直径为8厘米的五个环组成,其中两两相交的小曲边四边形(阴影部分)的面积都相等,已知五个圆环盖住的面积是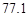 平方厘米,求每个小曲边四边形的面积.(
平方厘米,求每个小曲边四边形的面积.(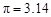 )
)
已知正方形 的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连擎起来得右图.那么,图中阴影部分的总面积等于多少平方厘米.(
的边长为10厘米,过它的四个顶点作一个大圆,过它的各边中点作一个小圆,再将对边中点用直线连擎起来得右图.那么,图中阴影部分的总面积等于多少平方厘米.( )
)
如图,ABCD是边长为a的正方形,以AB、BC、CD、DA分别为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.( 取3)
取3)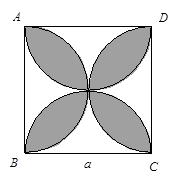
在桌面上放置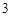 个两两重叠、形状相同的圆形纸片.它们的面积都是
个两两重叠、形状相同的圆形纸片.它们的面积都是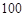 平方厘米,盖住桌面的总面积是
平方厘米,盖住桌面的总面积是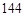 平方厘米,
平方厘米,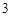 张纸片共同重叠的面积是
张纸片共同重叠的面积是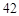 平方厘米.那么图中
平方厘米.那么图中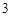 个阴影部分的面积的和多少是平方厘米?
个阴影部分的面积的和多少是平方厘米?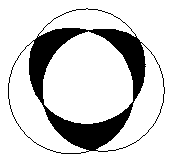
如图所示, 是一边长为
是一边长为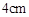 的正方形,
的正方形,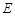 是
是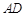 的中点,而
的中点,而 是
是 的中点.以
的中点.以 为圆心、半径为
为圆心、半径为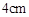 的四分之一圆的圆弧交
的四分之一圆的圆弧交 于
于 ,以
,以 为圆心、半径为
为圆心、半径为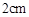 的四分之一圆的圆弧交
的四分之一圆的圆弧交 于
于 点,若图中
点,若图中 和
和 两块面积之差为
两块面积之差为 (其中
(其中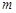 、
、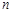 为正整数),请问
为正整数),请问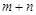 之值为何?
之值为何?

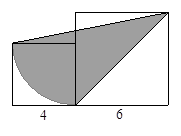
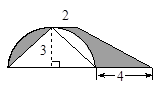
如图,矩形ABCD中,AB 6厘米,BC
6厘米,BC 4厘米,扇形ABE半径AE
4厘米,扇形ABE半径AE 6厘米,扇形CBF的半径CB
6厘米,扇形CBF的半径CB 4厘米,求阴影部分的面积.(
4厘米,求阴影部分的面积.( 取3)
取3)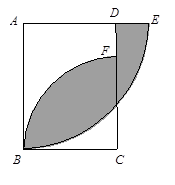
一个长方形的长为9,宽为6,一个半径为l的圆在这个长方形内任意运动,在长方形内这圆无法运动到的部分,面积的和是多少.( 取3)
取3)
如图,等腰直角三角形ABC的腰为10;以A为圆心,EF为圆弧,组成扇形AEF;两个阴影部分的面积相等.求扇形所在的圆面积.
大圆半径为 ,小圆半径为
,小圆半径为 ,两个同心圆构成一个环形.以圆心
,两个同心圆构成一个环形.以圆心 为顶点,半径
为顶点,半径 为边长作一个正方形:再以
为边长作一个正方形:再以 为顶点,以
为顶点,以 为边长作一个小正方形.图中阴影部分的面积为
为边长作一个小正方形.图中阴影部分的面积为 平方厘米,求环形面积.(圆周率取
平方厘米,求环形面积.(圆周率取 )
)
图中大正方形边长为 ,将其每条边进行三等分,连出四条虚线,再将虚线的中点连出一个正方形(如图),在这个正方形中画出一个最大的圆,则圆的面积是多少?(
,将其每条边进行三等分,连出四条虚线,再将虚线的中点连出一个正方形(如图),在这个正方形中画出一个最大的圆,则圆的面积是多少?( )
)
如下图所示,两个相同的正方形,左图中阴影部分是9个圆,右图中阴影部分是16个圆.哪个图中阴影部分的面积大?为什么?
如图,在 方格表中,分别以
方格表中,分别以 、
、 、
、 为圆心,半径为3、2、1,圆心角都是
为圆心,半径为3、2、1,圆心角都是 的三段圆弧与正方形
的三段圆弧与正方形 的边界围成了两个带形,那么这两个带形的面积之比
的边界围成了两个带形,那么这两个带形的面积之比


某仿古钱币直径为 厘米,钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图).求钱币在桌面上能覆盖的面积为多少?
厘米,钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图).求钱币在桌面上能覆盖的面积为多少?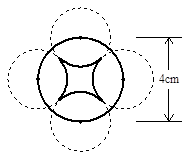
传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米.每当太阳西下,钟面就会出现奇妙的阴影(如右图).那么,阴影部分的面积是多少平方米.

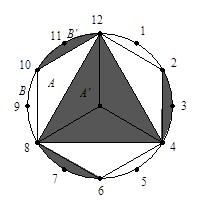
如图所示,两条线段相互垂直,全长为30厘米.圆紧贴直线从一端滚动到另一端(没有离开也没有滑动).在圆周上设一个定点 ,点
,点 从圆开始滚动时是接触直线的,当圆停止滚动时也接触到直线,而在圆滚动的全部过程中点
从圆开始滚动时是接触直线的,当圆停止滚动时也接触到直线,而在圆滚动的全部过程中点 是不接触直线的.那么,圆的半径是多少厘米?(设圆周率为3.14,除不尽时,请四舍五入保留小数点后两位.如有多种答案请全部写出)
是不接触直线的.那么,圆的半径是多少厘米?(设圆周率为3.14,除不尽时,请四舍五入保留小数点后两位.如有多种答案请全部写出)

将一块边长为 厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,求剪成的正方形铁皮的面积的最大值.
厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮,求剪成的正方形铁皮的面积的最大值.
图1 图2 图3
正三角形 的边长是6厘米,在一条直线上将它翻滚几次,使
的边长是6厘米,在一条直线上将它翻滚几次,使 点再次落在这条直线上,那么
点再次落在这条直线上,那么 点在翻滚过程中经过的路线总长度是多少厘米?如果三角形面积是15平方厘米,那么三角形在滚动过程中扫过的面积是多少平方厘米?(结果保留
点在翻滚过程中经过的路线总长度是多少厘米?如果三角形面积是15平方厘米,那么三角形在滚动过程中扫过的面积是多少平方厘米?(结果保留 )
)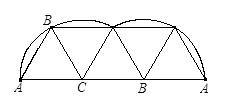
草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见如图).问:这只羊能够活动的范围有多大?(圆周率取 )
)
如图是一个直径为 的半圆,让这个半圆以
的半圆,让这个半圆以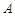 点为轴沿逆时针方向旋转
点为轴沿逆时针方向旋转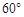 ,此时
,此时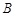 点移动到
点移动到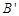 点,求阴影部分的面积.(图中长度单位为
点,求阴影部分的面积.(图中长度单位为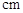 ,圆周率按
,圆周率按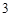 计算).
计算).
如图所示,直角三角形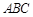 的斜边
的斜边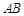 长为10厘米,
长为10厘米,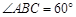 ,此时
,此时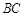 长5厘米.以点
长5厘米.以点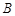 为中心,将
为中心,将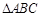 顺时针旋转
顺时针旋转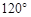 ,点
,点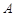 、
、 分别到达点
分别到达点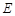 、
、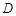 的位置.求
的位置.求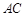 边扫过的图形即图中阴影部分的面积.(
边扫过的图形即图中阴影部分的面积.(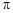 取3)
取3)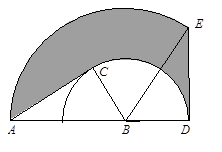
半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?
如图,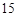 枚相同的硬币排成一个长方形,一个同样大小的硬币沿着外圈滚动一周,回到起始位置.问:这枚硬币自身转动了多少圈?
枚相同的硬币排成一个长方形,一个同样大小的硬币沿着外圈滚动一周,回到起始位置.问:这枚硬币自身转动了多少圈?
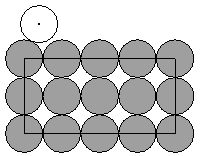
一枚半径为1 的圆形硬币相互紧靠着平放在桌面上,让一枚硬币沿着它们的外轮廓滚过后回到原来的位置,那么与原
的圆形硬币相互紧靠着平放在桌面上,让一枚硬币沿着它们的外轮廓滚过后回到原来的位置,那么与原 点重合的点是______.硬币自己转动______,硬币圆心的运动轨迹周长为_______.
点重合的点是______.硬币自己转动______,硬币圆心的运动轨迹周长为_______.

先做一个边长为 的等边三角形,再以三个顶点为圆心,
的等边三角形,再以三个顶点为圆心, 为半径作弧,形成曲边三角形(如左图).再准备两个这样的图形,把一个固定住(右图中的阴影),另一个围绕着它滚动,如右图那样,从顶点相接的状态下开始滚动.请问此图形滚动时经过的面积是多少平方厘米?(
为半径作弧,形成曲边三角形(如左图).再准备两个这样的图形,把一个固定住(右图中的阴影),另一个围绕着它滚动,如右图那样,从顶点相接的状态下开始滚动.请问此图形滚动时经过的面积是多少平方厘米?( )
)

如图,大圆半径为小圆的直径,已知图中阴影部分面积为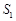 ,空白部分面积为
,空白部分面积为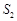 ,那么这两个部分的面积之比是多少?(圆周率取
,那么这两个部分的面积之比是多少?(圆周率取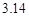 )
)
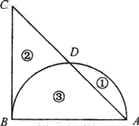
一块圆形稀有金属板平分给甲、乙二人.但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块.现甲取②、③两块,乙取①、④两块.如果这种金属板每平方厘米价值1000元,问:甲应偿付给乙多少元?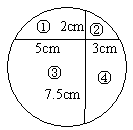
传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米.每当太阳西下,钟面就会出现奇妙的阴影(如左下图).那么,阴影部分的面积是多少平方米?
直角三角形 放在一条直线上,斜边
放在一条直线上,斜边 长
长 厘米,直角边
厘米,直角边 长
长 厘米.如下图所示,三角形由位置Ⅰ绕
厘米.如下图所示,三角形由位置Ⅰ绕 点转动,到达位置Ⅱ,此时
点转动,到达位置Ⅱ,此时 ,
, 点分别到达
点分别到达 ,
, 点;再绕
点;再绕 点转动,到达位置Ⅲ,此时
点转动,到达位置Ⅲ,此时 ,
, 点分别到达
点分别到达 ,
, 点.求
点.求 点经
点经 到
到 走过的路径的长.
走过的路径的长.
如图,一条直线上放着一个长和宽分别为 和
和 的长方形Ⅰ.它的对角线长恰好是
的长方形Ⅰ.它的对角线长恰好是 .让这个长方形绕顶点
.让这个长方形绕顶点 顺时针旋转
顺时针旋转 后到达长方形Ⅱ的位置,这样连续做三次,点
后到达长方形Ⅱ的位置,这样连续做三次,点 到达点
到达点 的位置.求点
的位置.求点 走过的路程的长.
走过的路程的长.
如右图,以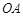 为斜边的直角三角形的面积是24平方厘米,斜边长10厘米,将它以
为斜边的直角三角形的面积是24平方厘米,斜边长10厘米,将它以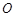 点为中心旋转
点为中心旋转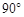 ,问:三角形扫过的面积是多少?(
,问:三角形扫过的面积是多少?(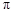 取3)
取3)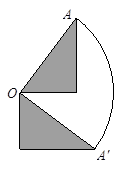
如果半径为25厘米的小铁环沿着半径为50厘米的大铁环的外侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?
如图所示,大圆周长是小圆周长的 (
( )倍,当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又回到原来的位置,小圆绕自己的圆心转动了几周?
)倍,当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又回到原来的位置,小圆绕自己的圆心转动了几周?
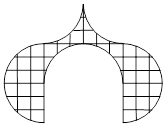
 8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整个方格纸面积的几分之几?
8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整个方格纸面积的几分之几?

 取
取 )
)
 ,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取
,三个圆两两相交于圆心.求阴影部分的面积和.(圆周率取 )
)



 )
)


 是正方形,且
是正方形,且 ,求阴影部分的面积.(取
,求阴影部分的面积.(取 )
)
 的长是
的长是 ,则阴影部分的面积是多少
,则阴影部分的面积是多少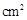 .(
.(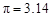 )
)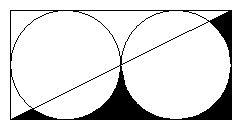
 的图中有两条互相垂直的线段,阴影部分面积
的图中有两条互相垂直的线段,阴影部分面积 与其它部分面积
与其它部分面积 之差(大减小)是多少
之差(大减小)是多少 .
.
 取3)
取3)
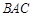 的面积是半圆
的面积是半圆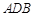 面积的
面积的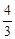 倍,则角
倍,则角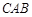 的度数是多少?
的度数是多少?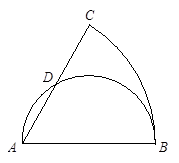
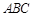 的两条直角边分别长
的两条直角边分别长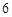 和
和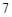 ,分别以
,分别以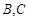 为圆心,
为圆心,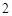 为半径画圆,已知图中阴影部分的面积是
为半径画圆,已知图中阴影部分的面积是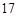 ,那么角
,那么角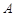 是多少度(
是多少度( )
)
 取3)
取3)


 取3)
取3)
 )
)
 是等腰直角三角形,
是等腰直角三角形, 是半圆周的中点,
是半圆周的中点, 是半圆的直径.已知
是半圆的直径.已知 ,那么阴影部分的面积是多少?(圆周率取
,那么阴影部分的面积是多少?(圆周率取 )
)
 )
)



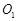 、
、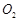 、
、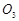 为圆心,求阴影部分的面积.(
为圆心,求阴影部分的面积.(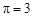 )
)
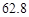 平方厘米,求阴影部分的面积.(
平方厘米,求阴影部分的面积.( )
)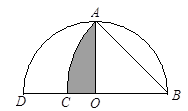
 ,阴影甲的面积比阴影乙的面积大7,求BC长.(
,阴影甲的面积比阴影乙的面积大7,求BC长.( )
)
 ,求阴影部分的面积.
,求阴影部分的面积.
 取3)
取3)
 ,它的内部放了一个半圆,图中阴影部分的面积为多少?
,它的内部放了一个半圆,图中阴影部分的面积为多少?
 取
取 )
)
 ,两个顶点正好在圆心上,求图形的总面积是多少?(圆周率取
,两个顶点正好在圆心上,求图形的总面积是多少?(圆周率取 )
)
 与
与 是两条垂直的直径,圆
是两条垂直的直径,圆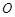 的半径为15厘米,
的半径为15厘米,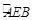 是以
是以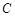 为圆心,
为圆心,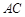 为半径的圆弧,求阴影部分面积.
为半径的圆弧,求阴影部分面积.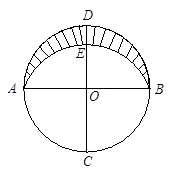
 是以C为圆心,AC为半径的圆弧.求阴影部分面积.
是以C为圆心,AC为半径的圆弧.求阴影部分面积.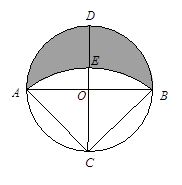
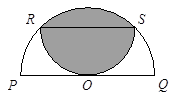
 和
和 是两个半圆.
是两个半圆.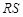 平行于
平行于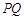 .如果大半圆的半径是1米,那么阴影部分是多少平方米?(
.如果大半圆的半径是1米,那么阴影部分是多少平方米?(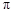 取
取 )
)
 中,对角线
中,对角线 长2厘米.扇形
长2厘米.扇形 是以
是以 为圆心,以
为圆心,以 为半径的圆的一部分. 求阴影部分的面积.
为半径的圆的一部分. 求阴影部分的面积.

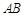 弦约等于17厘米,半径为10厘米,求阴影部分的面积.
弦约等于17厘米,半径为10厘米,求阴影部分的面积.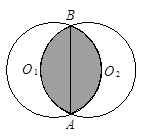
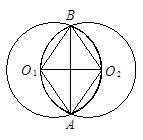
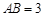 ,阴影部分的面积是
,阴影部分的面积是 
 是平行四边形,
是平行四边形,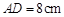 ,
,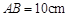 ,
, ,高
,高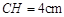 ,弧
,弧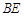 、
、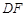 分别以
分别以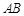 、
、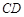 为半径,弧
为半径,弧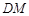 、
、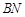 分别以
分别以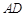 、
、 为半径,则阴影部分的面积为多少?(精确到
为半径,则阴影部分的面积为多少?(精确到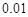 )
)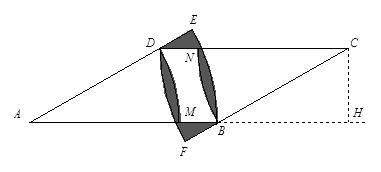
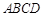 是一个长为
是一个长为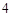 ,宽为
,宽为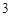 ,对角线长为
,对角线长为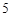 的正方形,它绕
的正方形,它绕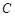 点按顺时针方向旋转
点按顺时针方向旋转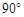 ,分别求出四边扫过图形的面积.
,分别求出四边扫过图形的面积.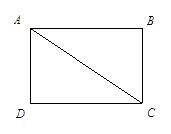





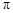 取近似值
取近似值 .
.
 ).
).
 、
、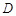 是以
是以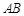 为直径的半圆的三等分点,
为直径的半圆的三等分点,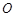 是圆心,且半径为6.求图中阴影部分的面积.
是圆心,且半径为6.求图中阴影部分的面积.
 取3)
取3)
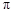 取3)
取3)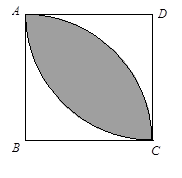
 )
)

 )
)
 取
取 )
)
 是直角三角形,阴影
是直角三角形,阴影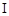 的面积比阴影
的面积比阴影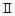 的面积小
的面积小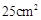 ,
,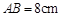 ,求
,求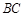 的长度.
的长度.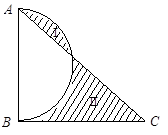
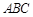 是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,
是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,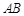 长40厘米.求
长40厘米.求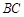 的长度?(
的长度?(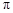 取
取 )
)
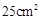 ,求圆环的面积.
,求圆环的面积.
 取
取 )
)
 ,请问阴影部分的面积为多少平方厘米?(取
,请问阴影部分的面积为多少平方厘米?(取 )
)

 是边长为26厘米的正三角形,圆
是边长为26厘米的正三角形,圆 的半径为
的半径为 厘米.
厘米. .求阴影部分的面积.
.求阴影部分的面积.

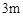 的等边三角形建筑物的墙角上(如图),绳长是
的等边三角形建筑物的墙角上(如图),绳长是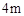 ,求狗所能到的地方的总面积.(圆周率按
,求狗所能到的地方的总面积.(圆周率按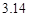 计算)
计算)
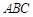 中,
中,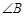 为直角,且
为直角,且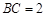 厘米,
厘米,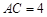 厘米,则在将
厘米,则在将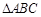 绕
绕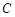 点顺时针旋转
点顺时针旋转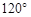 的过程中,
的过程中,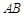 边扫过图形的面积为多少.(
边扫过图形的面积为多少.(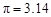 )
)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号