2022年湖南省益阳市中考数学试卷
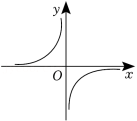
已知一个函数的因变量 与自变量 的几组对应值如表,则这个函数的表达式可以是( )
|
x |
… |
﹣1 |
0 |
1 |
2 |
… |
|
y |
… |
﹣2 |
0 |
2 |
4 |
… |
| A. |
|
B. |
|
C. |
|
D. |
|
在某市组织的物理实验操作考试中,考试所用实验室共有 个测试位,分成 组,同组 个测试位各有一道相同试题,各组的试题不同,分别标记为 ,考生从中随机抽取一道试题,则某个考生抽到试题 的概率为( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图1所示,将长为 的矩形纸片沿虚线折成 个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中 的值可以是( )

| A. |
|
B. |
|
C. |
|
D. |
|
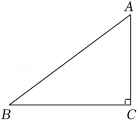
如图,在 中, ,点 是 上一点, ,连接 ,过点 作 ,交 的延长线于点 ,则 的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
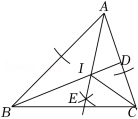
如图,在 中, 平分 ,以点 为圆心,以任意长为半径画弧交射线 于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点 ,作射线 ,交 于点 ,连接 ,以下说法错误的是( )
| A. |
到 边的距离相等 |
| B. |
平分 |
| C. |
是 的内心 |
| D. |
到 三点的距离相等 |
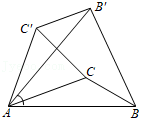
如图,已知 中, ,将 绕 点逆时针旋转 得到 ,以下结论:① ,② ,③ ,④ ,正确的有( )
| A. |
①②③ |
B. |
①②④ |
C. |
①③④ |
D. |
②③④ |
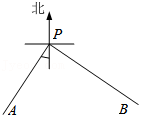
如图, 表示以 为起点的两条公路,其中公路 的走向是南偏西 ,公路 的走向是南偏东 ,则这两条公路的夹角 _____ .
近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多.为了解南迁到该区域某湿地的A种候鸟的情况,从中捕捉 只,戴上识别卡并放回;经过一段时间后观察发现, 只A种候鸟中有 只佩有识别卡,由此估计该湿地约有_____只A种候鸟.
如图,将边长为 的正方形 沿其对角线 平移,使 的对应点 满足 ,则所得正方形与原正方形重叠部分的面积是_____.

如图,直线 与 轴交于点 ,点 关于 轴的对称点为 ,经过点 和 轴上的点 的直线设为 .
(1)求点 的坐标;
(2)确定直线 对应的函数表达式.

为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为 分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
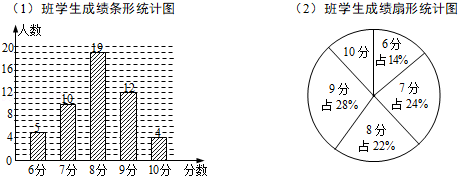
(1)求(2)班学生中测试成绩为 分的人数;
(2)请确定下表中 的值(只要求写出求 的计算过程);
|
统计量 |
平均数 |
众数 |
中位数 |
方差 |
|
(1)班 |
8 |
8 |
c |
1.16 |
|
(2)班 |
a |
b |
8 |
1.56 |
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
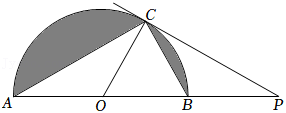
如图, 是圆 被直径 分成的半圆上一点,过点 的圆 的切线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,求 的度数;
(3)在(2)的条件下,若 ,求图中阴影部分的面积(结果保留 和根号).
在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割比赛.已知乙每小时收割的亩数比甲少 ,两人各收割 亩水稻,乙则比甲多用 小时完成任务;甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为 .
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?
(2)某水稻种植大户有与比赛中规格相同的 亩待收水稻,邀请甲、乙两人操控原收割机一同前去完成收割任务,要求平均损失率不超过 ,则最多安排甲收割多少小时?
如图,在平面直角坐标系 中,抛物线 的顶点 在抛物线 上,直线 与抛物线 分别交于点 .
(1)求 的值;
(2)将 的纵坐标分别记为 ,设 ,若 的最大值为 ,则 的值是多少?
(3) 是 轴的正半轴上一点,且 的中点 恰好在抛物线 上.试探究:此时无论 为何负值,在 轴的负半轴上是否存在定点 ,使 总为直角?若存在,请求出点 的坐标;若不存在,请说明理由.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号